Describing protein motions with nonlinear dimensionality reduction
Twenty years ago, commenting on macromolecular dynamics, Francis Crick wrote that “what seems to physicists a hopelessly complicated process may have been what Nature found simplest.” Indeed, if one uses molecular dynamics simulations (that follow the molecular motion of biological systems in the high dimensional Cartesian space spanned by each and all atomic degrees of freedom) the behavior of a macromolecular system may appear overwhelmingly complicated: the shear amount of data and parameters generated does not allow a direct and efficient interpretation and understanding of the results in terms of new fundamental principles, i.e., “what Nature found simplest”.
In the fall of 2005, the Institute for Pure and Applied Mathematics (IPAM) held a 3-month program on Bridging Time and Length Scales in Materials Science and Bio-Physics, that brought together a mix of pure and applied mathematicians, material scientists, biophysicists, and computer scientists. One of the goals of the program was to address the description of the dynamics of large molecules, and how it relates to other problems in materials sciences and mathematics. Among the participants were Cecilia Clementi and several members of her research group, including her student Payel Das. Clementi is a leader in computational biophysics, who has recently proposed a new approach that could be used to understand if and how relatively simple and general organizational principles emerge from the interactions of the single degrees of freedom. Crucial steps towards the understanding of the dynamics of a macromolecule (such as the folding of a protein) are a rigorous analysis of the effective dimensionality, and the definition of the minimal set of physically relevant variables to describe such a complex process. The first results in this context have been obtained in collaboration between Cecilia Clementi’s and Lydia Kavraki’s groups at Rice University.
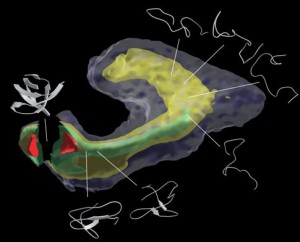
Clementi and Kavraki showed that a few global coordinates for the characterization of protein folding reactions can be obtained by using nonlinear dimensionality reduction methods. This is illustrated in the figure, which shows the low dimensional representation of the free energy landscape of a protein folding reaction, as emerging from non-linear dimensionality reduction. The green isosurface identifies the lowest free energy route from the unfolded state to the folded state (from right to left). The folded state corresponds to the global free energy minimum (red isosurface). These results show that non-linear dimensionality reduction techniques can efficiently find a low dimensional representation that captures the overall dynamics of a complex process such as protein folding. More details can be found in P. Das, M. Moll, H. Stamati, L.E. Kavraki, & C.Clementi, Proc. Natl. Acad. Sci. USA 103, 9885-9890 (2006).
The IPAM program provided the perfect environment for Clementi to begin investigating the more mathematical and fundamental aspects of the problem. Clementi’s group started several new collaborations during the program. In particular, Clementi is now working with Mauro Maggioni (Duke University) to use multiscale geometric measure theory and harmonic analysis to extract the effective dimensionality of large biomolecular complexes and self-assembly processes, its dependence on time and space, and the connection of the observed effective low-dimensional dynamics to the variation of global physical parameters.