By Andrew Papanicolaou

The technique of volatility trading has been common practice since the 1970’s. Typically, a long (short) position in volatility included a long (short) position in options. In 2003 there came a more standardized way of trading volatility, as the VIX formula became the universally-accepted predictor of volatility. The VIX is a 30-day predictor of volatility given by a weighted portfolio of out-of-the-money European options on the S&P500 (see Demeterfi, et al. 1999),

\(VIX= \sqrt{\frac{2e^{r \,\! \tau}}{\tau} \left(\int_{0}^{F} \frac{P(K)}{K^2} dK + \int_F^{\infty} \frac{C(K)}{K^2} dK \right)}\)

where \(τ = 30\) days, \(r ≥ 0\) is the risk-free rate, F is the 30-day forward price on the S&P500, and with \(P(K)\) and \(C(K)\) being respective prices for puts and calls with strike and 30 days to maturity. An important thing to notice in the VIX formula is how it’s composed entirely of option premia (i.e. out-of-the-money options have no intrinsic value) and hence trading VIX is like trading the premium that is priced into the options market. A common practice is to hedge high volatility with long positions in derivatives on the VIX itself. For example, the Chicago Board Options Exchange uses long positions in VIX call options to produce their VIX Tail Hedge Index, an index which historically has performed better than several benchmarks (Chicago Board Options Exchange (CBOE) 2011).

The VIX was among the topics discussed at IPAM’s Spring 2015 program “Broad Perspectives and New Directions in Financial Mathematics”, with the goal of finding ways to bring greater stability into banking systems, algorithmic trading, and commodities markets. There are countless models for pricing and hedging of derivative products, but for IPAM participants it was the model parameters implied by market prices that were of primary interest. In particular, VIX is an implied volatility parameter that quantifies fear/optimism among traders, and in the past has been a strong indication of any stress or impending crisis.

A contemporary problem in this area during Spring of 2015 was in the establishment of links between markets for VIX derivatives and the primary securities (i.e. no VIX products; only S&P500, S&P500 options, low-risk bonds, etc….) (Carr and Wu 2006). Relative to the market sub-space spanned by primary securities, VIX derivatives provide a new dimension of hedgability because buying and selling of VIX previously was not possible. Figure 1 illustrates the added dimension relative to the sub-space of primary securities. A new result that was produced at IPAM was the linking of the two markets with the so-called time-spread portfolio –a portfolio that is long in the spreads between 1-month and 2-month S&P500 put options (Papanicolaou 2016). The time-spread portfolio is part of a term-structure on volatility composed entirely with primary market securities, and is a non-null component of the primary market sub-space that is also present in VIX derivatives (see the red line in Figure 1). Hence, the time-spread portfolio links the two markets by providing a robust/model-free component that is common to both market subspaces.

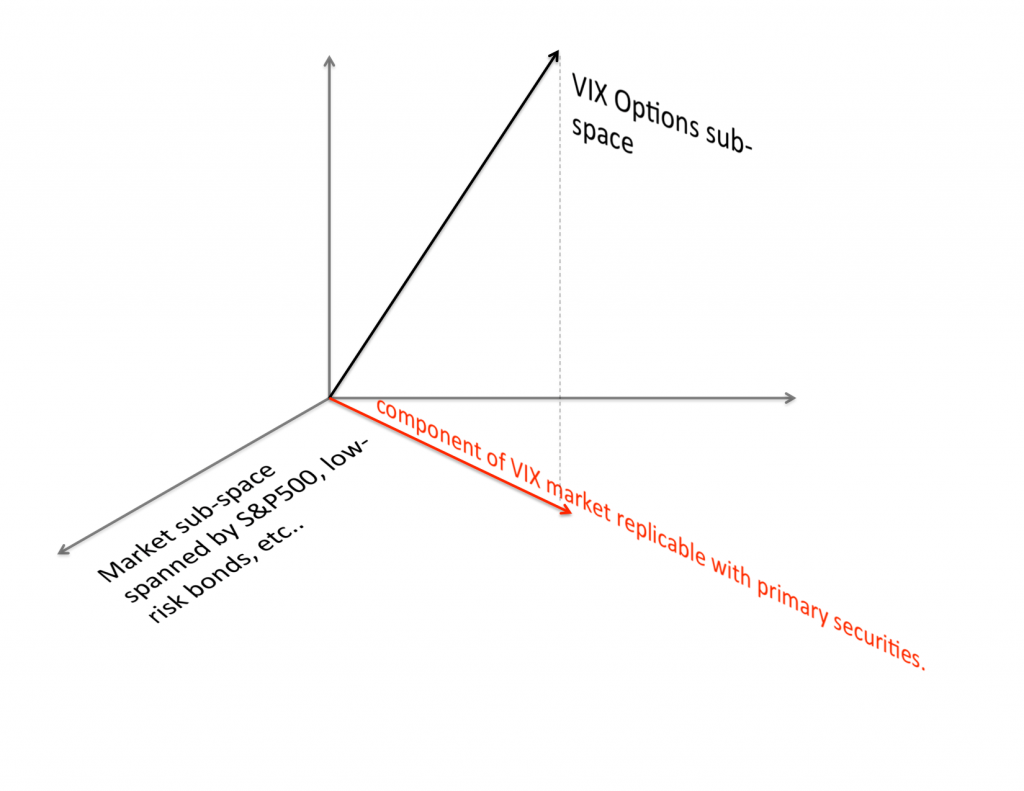
Figure 1: The horizontal place is the market sub-space spanned by primary securities, and the vertical direction is the market sub-space created by VIX options. The red line represents the projection of the VIX-options component onto the primary sub-space.

The 2015 program was a movement toward a deeper analysis of financial data and making new discoveries about information implied by financial markets. Thanks to the efforts of the program’s participants, the future of the financial system will be less uncertain with an increased understanding of market dynamics and financial risk.

Works Cited

Carr, P., and L. Wu. “A Tale of Two Indices.” The Journal of Derivatives 13, no. 3 (2006): 13-29.

Chicago Board Options Exchange (CBOE). White paper: CBOE VIX tail hedge index (ticker VXTH). Available at http://www.cboe.com/micro/vxth/ documents/vxthwhitepaper.pdf., 2011.

Demeterfi, K., E. Derman, M. Kamal, and J. Zou. “More Then You Ever Wanted to Know About Volatility Swaps.” The Journal of Deriviatives 6, no. 4 (1999): 9-32.

Papanicolaou, A. “Analysis of VIX Markets with a Time-Spread Portfolio.” (under review with journal) (available at http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2618933.), 2016: 1-35.