The Kakeya problem
Submitted by Larry Guth (MIT)
The Kakeya problem is an open problem in Euclidean geometry, and it was a central theme in the 2014 IPAM long program, Algebraic Techniques for Combinatorial and Computational Geometry. It is elementary to state, but it’s also a model for deep open questions in Fourier analysis. Different approaches to the problem have involved tools and ideas from many subfields of mathematics, such as geometric combinatorics, multiscale analysis, number theory, and algebraic geometry. These different approaches have produced interesting partial results or solved related problems, but the original problem remains open.
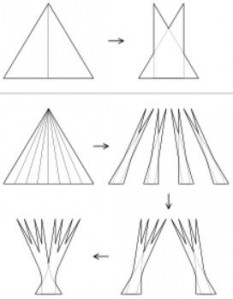
The Kakeya problem has to do with thin cylinders pointing in noticeably different directions, in the sense that the angular separation between directions is larger than the angular width of each cylinder. In the early 20th century, Besicovitch found a surprising construction (illustrated in Figure 1) to compress the cylinders into a somewhat small set (whose volume goes to zero at a logarithmic rate when the thickness of the cylinders go to zero). The Kakeya problem asks if one can compress the cylinders into a much smaller set (where the volume goes to zero at a polynomial rate).
The Kakeya problem naturally arises in physics problems. For example, an airplane traveling at the speed of sound in a straight line generates sound waves that propagate at the same speed as the airplane. The sound accumulates — if the plane has been traveling from time 0 to 10, then the sound waves generated between 0 and 10 are all present, vibrating the airplane at time 10 — to form a “wave train.” The sound dies off away from the airplane, so that the sound waves are strongest in a cylinder (in space-time) around the path of the airplane. Important unanswered questions about wave propagation (as well as Fourier analysis and partial differential equations) are related to how wave trains could interact with each other. And this in turn is related to how tubes in different directions can overlap. See [1] for more details.
Recently, Zeev Dvir gave an elegant solution [2] to a cousin of the Kakeya problem, coming from number theory. Instead of the real numbers, it involves the field of integers modulo a prime p: Zp. The theorem states that a subset of Zpn containing a line in every direction must contain a large number (of size np) of points. The proof came as a great surprise, because it uses tools from algebra and computer science, namely high degree polynomials and error-correcting codes.
One aim of the IPAM program was to see how much these new tools can say about the original Kakeya problem. Can this approach give us new estimates about cylinders and waves? So far, it’s too early to say.
REFERENCES