Mathematics and Physics at the Moiré Scale
The unique electronic, optical, and mechanical properties of 2D materials have recently sparked an extraordinary level of experimental, theoretical, and computational activity in the materials science and physics communities. Interest in the mathematics community has recently emerged to develop rigorous foundations, improved models, and computational methods. IPAM sponsored a workshop on “Theory and Computation for 2D Materials” during January 13-17, 2020 that facilitated exchanges between the mathematics community and the physics communities working on 2D materials.
Intense interest in 2D materials was sparked by the exfoliation of graphene, a single layer of carbon atoms with hexagonal structure by Geim and Novoselov in 2004. Graphene had previously been theoretically shown by Wallace (1947) to have a linear dispersion near conical Dirac points and later shown to have quasi-particles that propagate by a massless Dirac equation for a two-component wave function (in analogy to Dirac’s relativistic equation with four-component wave functions that propagate at the speed of light). This analogy to Dirac’s relativistic equation has recently motivated the exploration of phenomena such as Klein’s paradox in graphene. A rigorous and general approach by Weinstein and Fefferman to the derivation of the massless Dirac equation for the long wave, low energy wave packets in hexagon structures was presented by Michael Weinstein and an application to the investigation of edge states was presented by Alexis Druhot and Alexander Watson.
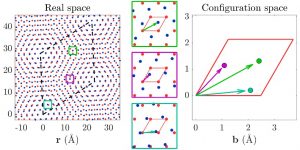
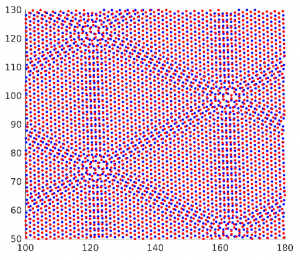
Placing a two-dimensional lattice on another with a small rotation gives rise to periodic “moiré” patterns on a superlattice scale much larger than the original lattice analogous to the beating of two waves with slightly different wavelength (see twisted hexagonal lattices below left). This effective large-scale fundamental domain has opened the possibility of discovering new phenomena at the moiré scale that were previously inaccessible at the atomistic scale. An early example was the observation of the fractal Hofstadter butterfly in twisted bilayer graphene by Philip Kim, et al. (2013). Mitchell Luskin and Paul Cazeaux gave presentations describing their general mathematical theory of moiré patterns in relaxed incommensurate 2D heterostructures (see relaxation of twisted bilayer hexagonal lattices below right).
Rafi Bistrizter and Allan MacDonald (2010) developed a low energy continuum model for the electronic structure of twisted bilayer graphene at the moiré scale and showed that the group velocity of electronic quasi-particles is nearly zero at a “magic” angle of approximately 1°, when the interlayer coupling balances the separation of the Dirac cones of the twisted bilayer. This low group velocity and the localization of the electron density led Bistrizter and MacDonald to suggest that correlated electronic phases such as unconventional superconductivity and Mott insulation might be observed in magic angle twisted bilayer graphene. Such an observation (2018) by Pablo Jarillo-Herrero’s group galvanized the scientific world and has led to an intense synergistic development and investigation of new correlated physics models in parallel with experimental investigations.
MacDonald gave an overview of his recent research on the electronic and optical properties of 2D moiré superlattices and Francisco Guinea, another pioneer in the theory of 2D materials, gave a presentation on electron-electron interactions in graphene systems. Theorists and mathematicians gave lectures on Wannier functions for 2D layered materials (Shiang Fang), band-free approaches (Stephen Carr), and momentum space methods for relaxed incommensurate bilayers (Daniel Massatt).
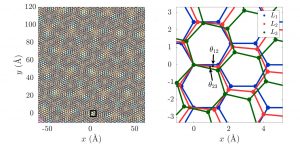
Novel 2D heterostructures beyond twisted bilayer graphene are actively being investigated in the search for new platforms for correlated physics. Zoe Zhu gave theory and computation for twisted trilayer graphene (see figure below) that highlighted the challenges presented by moiré of moiré structures. Experimental results demonstrating correlated phenomena for twisted trilayer graphene were then presented by Ke Wang.
Mathematics and physics at the moiré scale continues to be intensely investigated and has been a major theme in the IPAM long program on Advancing Quantum Mechanics with Mathematics and Statistics. An informal mini workshop will be held during May 18-20, 2022.