Overcoming the Curse of Dimensionality for Control Theory
Optimal control problems lead to Hamilton-Jacobi Bellman (HJB) differential equations in many space variables for finding the cost function to be optimized. This beautiful connection has not generally led to effective numerical methods because grid based solutions of partial differential equations in n variables generally have memory requirements and complexity that is exponential in n. This is the “curse of dimensionality” a term coined by Richard Bellman in 1957.
Jerome Darbon and Stanley Osher were motivated to think about high-dimensional problems in control theory by lectures of Claire Tomlin and William McEneaney that they heard at IPAM. Recently they noticed a link between HJB equations and certain currently very popular convex optimization problems. They proposed and tested a new approach borrowing ideas from \(ℓ_1\) regularized convex optimization problems arising in compressed sensing. By using the Hopf formula, derived in 1965 for solving HJB equations, and restricting the Hamiltonian to be convex and positively homogeneous degree one in the gradient, they needed to solve problems resembling the compressive sensing optimization mentioned above. This class includes linear controls involving time and for which the control set is compact and convex.
By using optimization ideas motivated by compressed sensing they obtained incredibly fast algorithms which do not use grids and hence have minimal memory requirements. For example if the Hamiltonian is the \(ℓ_2\) norm (not the square of this) of the gradient, this technique can be used to compute the distance to a compact convex set in 4, 8, 12, 16 dimensions with each function evolution taking \(10^{-7}\) seconds on a standard lap top. This means that 10 million points can be evaluated in a second. The accompanying figure shows the results of their method for a 2-dimensional slice at two different times for the HJB equation corresponding to the minimal distance to a union of two spheres in dimension 8.
Moreover, using a trick involving the level set method, they find the projection onto a convex compact set Ω for a given point in \(R^n \backslash Ω\) equally quickly. This is an important problem in its own right.
The applications to control theory, and hopefully differential games, and perhaps even new approaches to linear programming are expected to follow soon. The curse has been lifted a bit!
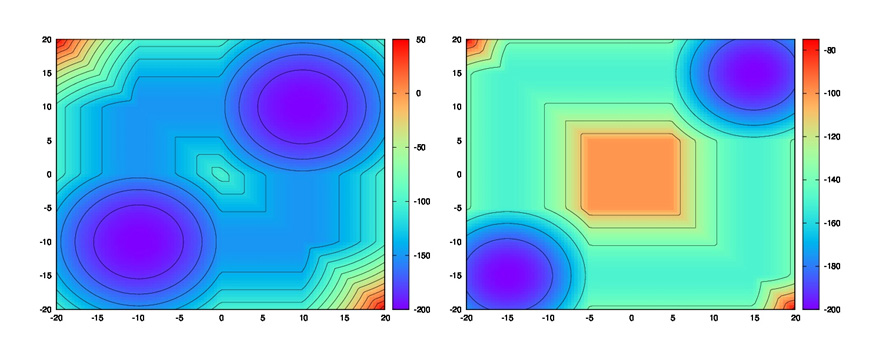
Figure 1: Evaluation of the solution of HJB for the distance to minimal distance to two spheres at times, t = 5 (left) and t = 10 (right).